研究经历
研究兴趣
我的研究兴趣是应用算法学,包括计算机算法的设计、分析、应用。
具体讲,研究网络、多媒体、生物信息学等领域中的关键算法问题。
我希望研究可以做到又好看、又好吃:理论上深刻、实践中有效。
第六部分 —计算蛋白质组学,pFind十年回顾
2020-9-10
第五部分 — 计算蛋白质组学,蛋白质鉴定搜索引擎pFind
2012-3-26
1997年我从清华大学计算机系博士毕业之后,先是做了两年DVB/MPEG-2数字电视传输与条件接收技术的研究,然后从中抽象出一个均匀复用问题并扩展到均匀交换问题,做了七年多均匀调度算法的研究。可以说,毕业十年基本上还是研究算法学问题。自2007年开始,我的研究方向有所变化,负责带领一个团队研究质谱鉴定蛋白质的问题。
所谓质谱鉴定蛋白质问题,就是给定一个生物样品,我们想鉴定其中包含哪些蛋白质成分。蛋白质分离、电离之后进入生物质谱仪,碎裂之后生成一个数字化的质谱图,其横轴是蛋白质片断离子的质量电荷比即质荷比,纵轴是离子强度计数,因此一个质谱图相当于一个直方图。我们要从这个数字化质谱图反推出生成它的蛋白质是什么。下面就是一台高精度生物质谱仪生成的一个质谱图。
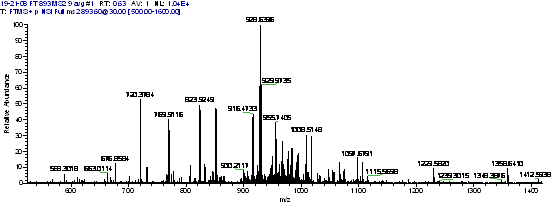
质谱仪很神奇,因为迄今为止已经有六位与质谱仪发明、发现相关的诺贝尔奖得主,而且如果各位熟悉基因组测序仪及其巨大威力的话,那么质谱仪就是蛋白质层次的测序仪。质谱仪也很平凡,因为就计算而言,它与数码相机、核磁共振仪、断层扫描仪没有本质区别,只是一种新的数字化仪器而已,而且质谱图看起来比图像还简单一些,因为图像一般是二维坐标下的强度图,而质谱图是一维坐标下的强度图。
质谱鉴定蛋白质,其实与图像处理、人脸识别没什么本质区别。不仅如此,质谱鉴定蛋白质与文本检索(比如我们常用的谷歌、百度检索)也高度相似。所有这些问题,都属于一个领域,就是信息检索。而我们团队的任务,就是研究一个特定的信息检索问题——质谱鉴定蛋白质,开发一个特定的搜索引擎——pFind。
pFind的命名中,p代表蛋白质(protein)或者蛋白质片段(peptide, 也称肽段),Find就是搜索、鉴定之意。pFind既是我们的搜索引擎名称,也是我们团队的名称,团队每个成员都是pFinder。pFind的Founder是高文教授,2002年他凭借人脸识别、手语识别等领域的工作基础成功申请到国家973项目“生命科学若干前沿与交叉问题研究”第7课题“基于信息技术的蛋白质组研究”,我负责实施并逐渐接手。这样算起来,pFind已经有接近10年的发展历史了。
那么,经过近10年的努力,pFind达到什么水平了?首先,自然是一系列文章的突破,大家可以看pFind网站Publications栏目所列,蛋白质组学三大国际期刊MCP、JPR、Proteomics,生物信息学国际期刊Bioinformatics,生物信息学国际会议ISMB,计算蛋白质组学国际会议RECOMB-CP,我们都已经突破,正在向PNAS、Nature Methods迈进。其次,是pFind系列软件的突破,大家可以看pFind网站首页所列Software,从核心引擎到预处理与后处理、从数据库搜索到从头测序、从单肽段鉴定到交联肽段鉴定、从定性鉴定到定量分析,丰富的软件工具形成一个平台,可以支持一个质谱/蛋白质组学实验室日常科研和服务工作。特别地,pFind软件成功鉴定核心岩藻糖化修饰蛋白质的工作发表在MCP, pNovo软件成功鉴定线虫纲精子活化标记蛋白质的工作发表在PNAS。第三,是国内外影响的扩大,大家可以看pFind网站Benchmark栏目,其中有我们几年来参加国际评测活动的信息;Collaborators栏目,其中有我们的国内外朋友和合作者的信息;CNCP栏目,其中有我们主办的首届中国计算蛋白质组学研讨会的信息;Download栏目,自2010年5月开放至2011年底,国内外注册下载pFind软件数目已经达到147套。
pFind当前的发展优势有多个方面。首先,时势造英雄,作为生物信息学比较年轻的一个新分支,以基于质谱技术的规模化蛋白质鉴定为核心内容的计算蛋白质组学及其应用正在国内外蓬勃发展;基因组测序的今天就是蛋白质鉴定的明天,断层扫描仪、核磁共振仪的今天就是生物质谱仪的明天。年轻时不犹豫,年老时才能不后悔。其次,经过近十年的持续努力,我们已经掌握了蛋白质鉴定搜索引擎设计与实现的完整技术,因此也就比较容易地实现了从常规单肽段鉴定到非常规的肽段交联鉴定的发展,再进一步的跨越相信也万变不离其宗。第三,我们与高水平的质谱/蛋白质组学团队有非常密切的合作,我们的工作态度和工作能力赢得了同行的信任,所以我们不断接触重要的问题、高质量的数据,合作产出高质量的文章,利用软件优势进一步服务国内外同行,推动本领域的良性发展。第四,我们背靠计算所,曙光、龙芯团队可以为我们提供集群、多核、众核等超级计算硬件支持,文本、多媒体、跨媒体信息检索团队可以为我们提供搜索引擎设计等核心软件技术支持,在这个技术平台支持下的pFind具有独特的竞争优势。第五,也是最重要的,我们的团队,特别是新一代pFinder快速成长,他们对本领域的前景充满信心,对于自己的作品充满自豪,这是pFind的希望所在;无论将来他们走到哪里,都将对中国计算蛋白质组学做出独特的贡献。
未来的十年,pFind团队将秉承“伤其十指,不如断其一指”的原则,继续做好pFind的算法、软件、推广。一个人,一个团队,一辈子能把一件事情做好、做透,已经很不容易了。希望不远的将来,中国的生物/质谱/蛋白质组学工作者可以放心地使用中国人自己的软件,使用自己的仪器,研究自己的问题,造福自己的同类。每一个领域,每一个职业,都有自己的责任,都有自己的尊严。我们欢迎有志气的青年学生加入pFind团队,开创属于自己的未来!
2012-3-26
第一部分 — 局部搜索方法的实验分析与设计
局部搜索方法是一类算法设计方法,非常简单,异常有效。通常的最优化方法(包括连续优化和组合优化),和计算智能方法(包括模拟退火、禁忌搜索、遗传算法、进化算法),本质上都是局部搜索方法。局部搜索方法的研究门槛不高,这些年计算智能、进化计算的研究像十年前一样热闹,但是个人认为,只有坚持走实验算法学(Experimental Algorithmics)的道路,才可能取得真正的成果。
我的博士论文第一、二章,以可满足性问题为例,详细介绍了我研究局部搜索方法的动机,我提出的实验分析方法,以及实例示范。为了进行这项研究,我申请延期毕业一年,直到毕业前最后一刻才真正获得突破,现在回想起来还惊心动魄。对于这项研究,我情有独钟,个人评价最高,多位评审老师也给出了高度评价,认为具有开创性。
这项工作由于毕业前夕刚刚完成,没有通过期刊、会议论文的形式发表。这是很大的遗憾,因为即使毕业已经十年,这项研究中的发现我相信仍然非常有价值。希望以后有机会重新回到这项研究工作,了却一桩心愿。
Local search methods dated back to 1970s when Shen Lin was trying to solve the Traveling Salesman Problem (TSP). An excellent survey and collection of theoretical research results appeared in Chapter 19 of Combinatorial Optimization written by Papadimitriou and Steiglitz in 1982. Though as simple as blind-person hill-climbing, local search was quite effective in practice and non-trivial in theory. Renaissance of local search methods is partly due to its success in solving million-queen problem within one minute around 1990, and partly due to emergence of some new variants with fashionable names such as simulated annealing, tabu search and genetic/evolutionary algorithms. A new book Local Search in Combinatorial Optimization in 1997 is an excellent and more up-to-date survey.
In my perspective, local search is the most promising approach to attacking the notorious NP-complete problems, and its research should be done in the spirit of Experimental Algorithmics. It seems to me that ad hoc local search research is now in a plateau, with no significant progress since 1994 in solving the satisfiability problem, for instance. A key enabling technology is a systematic and scientific suit of experimental analysis methods for local search, and my study is a step forward in this direction (refer to Chapters 2, better together with Chapter 1, of my PhD thesis), which reveals that many classic works on local search analysis, e.g., that of Johnson and McGeoch, might contain a systematic error.
May 1, 2003
第二部分 — 空间中均匀分布点集的构造
博士论文的第三章,分析空间点集的均匀划分性能,其中涉及一些复杂组合公式的证明。
引伸出的一个更为重要的问题是:高维组合空间的均匀采样点设计,例如n!个排列构成的空间中,如何选择k个排列,使之在整个空间中分布得非常均匀。
其重要性在于:对于大规模组合优化问题,精确求解不可能,只有通过有效采样才能得到满意解。直观上讲,越均匀的采样点集代表性越强,优化性能应当更好。
我国科学家张里千研究的正交设计,方开泰、王元研究的均匀设计,是在连续空间上的相同问题。组合空间上的问题不会更容易。我不肯定自己是否具有足够的功力。
但是至少可以设计空间采样点分布均匀性的直观合理定义,然后就可以采用局部搜索方法来优化初始点集的均匀性,即使其理论性能难以分析,其统计性能还是可以分析的,而且比较独立的是,此法实用性可能超出预想。
My interests in this problem dated back to my inadvertent solving of a partitioned-based initial points selection problem (refer to Chapter 3 of my PhD thesis), which proved that uniform partition is better than nonuniform partition. This was my first theoretical research result. A byproduct is a beautiful theorem conjectured by me but conquered by my maths teacher Prof. Xuguang Lu:
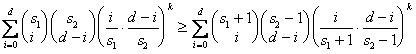 ,
,
where all parameters are non-negative integers, s1 £ s2 - 2, d £ s1 + s2. If you can derive a simple proof, drop me a message.
Later I tried to construct uniformly distributed point sets in space {0, 1}n. For instance, how to select 10 points in {0, 1}100 or 10 lattice points in [0, 1)100 which are distributed uniformly in the space? Most related researches are for continuous space [0, 1)n, e.g., discrepancy methods, uniform design, all of which are quite hot now; yet the corresponding problem in discrete spaces seems to be completely different and more general. Besides space {0, 1}n, another important discrete space is the space of permutations.
In fact, this is another optimization method, especially crucial in experiment design where computing an objective function on any one point is very expensive, e.g., an atomic bomb explosion under a specific parameter configuration.
May 1, 2003
第三部分 — 算法设计的可读性变换
研究算法设计的可读性变换,仍然来源于算法设计统一性或者系统化的考虑。
利用不同问题之间的关联性来求解问题是个自然的思路,一般都是把一个新问题设法变换到一个老问题形式,然后利用老问题已有的算法求解,最后把结果变换成原问题的解。这就是徐利治先生倡导的关系-映射-反演方法。但是很多情况下这并非是最理想的方法,比如数学证明虽然注重结果,但是一个内蕴证明更受青睐;或者不是最有效的方法,例如算法设计不仅仅要求结果正确,而且特别强调效率。
以组合优化问题求解为例,可满足性问题和旅行商问题原则上可以互相转化求解,但是把问题形式变化过去,难以充分表达、利用原问题的特性,最终也难以有效地求解。因此,真实情况是,把旅行商问题求解中发展起来的局部搜索方法抽象出来,应用到可满足性问题的算法设计。这就是我所说的算法变换或者可读性变换,即把旅行商问题的算法变换到可满足性问题,用可满足性问题的语言表达算法。
我在这个方向上的工作体现在用吴方法的可读性算法变换求解可满足性问题(博士论文第四章)。师叔评阅认为“作者极富创造性地提出可读性变换的概念及方法,在用吴方法求解SAT问题中,建立起求余运算与归结运算之间的对应关系,其形式之优美和简洁,使人耳目一新。用吴方法为求解SAT问题建立了一个全新的路子。这是一个极富创造性的工作。”
可读性算法变换为具体问题的算法研究开拓了思路。如有机会我将优先回到这个方向解决新问题。
When we come across a new problem, a common idea is to transform it into a familiar old problem with ready algorithms, then solve it, and finally transform the solution back to the new problem. This is called RMI method, namely relation, mapping, inversion, by Chinese mathematician Prof. Li-Zhi Xu. With this method, only heads and tails of the problem solving procedure are transformed, excluding the body — the algorithm. The algorithm is a blackbox to the new problem.
I propose the concept of algorithm transform or readable transform as a novel problem solving principle. In particular, it is a new algorithm design method. Instead of transforming the input of the new problem into the input of the old problem and then transforming the output (solution) of the old problem back into the output (solution) of the new problem, we transform the body of algorithm for the old problem into a new algorithm for the new problem. Now the new algorithm is in the language of the new problem and hence is readable.
With readable transform in mind, I investigated the problems of solving SAT by constraint satisfaction algorithms of AI and by Wu's method of polynomial equations solving (refer to Solving SAT by algorithm transform of Wu’s method, Journal of Computer Science and Technology, vol. 14, no. 5, Sept. 1999, pp. 468-480; or refer to Chapter 4 of my PhD thesis).
May 1, 2003
第四部分 — 均匀调度算法的设计、分析、应用
这项研究来源于一个真实问题——MPEG-2/DVB复用器设计。这是1999年底我和工程师一起吃午饭聊天时发现并抽象出来的。2002年我发现这个问题可以推广到高速路由器/交换机的交换结构设计中。解决实际问题一直是我的梦想,特别是我博士毕业后的梦想。
这项研究已经历时七年,是我博士毕业十年来最主要的研究经历。均匀性的概念非常基本,均匀调度在单机、并行多机、交换机上的实现非常具有挑战性。实话说,我真的低估了这些问题的难度,也低估了得到国际学术界同行认可的难度。
目前的主要结果是一篇会议文章,一篇期刊文章:
会议论文:Si-Min He, Shu-Tao Sun, et al. Smooth switching problem in buffered crossbar switches, ACM SIGMETRICS, pp. 386-387, 2005。目前为止,完全由大陆学者完成的工作,在这个1973年开始举办的ACM年度会议上仅仅发表过两篇短文,包括这一篇。当我参加会议注册时,组织会议的大陆学生很意外、也很高兴。
期刊论文:Si-Min He, Shu-Tao Sun, Hong-Tao Guan, et al. On guaranteed smooth switching for buffered crossbar switches, IEEE/ACM Trans. Networking, vol. 16, no. 3, pp. 718-731, June 2008。当时完全由大陆学者完成的工作,在这个期刊上仅仅发表过三篇文章;就交换结构(switch fabric)的研究而言,这可能是第一篇。
单机上的均匀调度问题有很多其他算法,对其均匀性的理论和实验分析计划单独成文总结。多机上的均匀调度问题更具有挑战性,曾经失败过多次。
研究论文
Si-Min He, Shu-Tao Sun, Hong-Tao Guan, Qiang Zheng, You-Jian Zhao, Wen Gao. On guaranteed smooth switching for buffered crossbar switches. IEEE/ACM Transactions on Networking, vol. 16, no. 3, pp. 718-731, June 2008.
Simin He, Shutao Sun, Wei Zhao, Yanfeng Zheng, Wen Gao. Smooth switching problem in buffered crossbar switches. ACM SIGMETRICS, pp. 386-387, Banff, Alberta, Canada, 2005.
HE Simin, ZHANG Bo. Solving SAT by algorithm transform of Wu’s method. Journal of Computer Science and Technology, Sept. 1999, 14(5): 468-480. Preliminary version was accepted by poster session of Int’l Joint Conf. Artificial Intelligence (IJCAI), 1997.
贺思敏, 张钹. 用吴方法求解可满足性问题II——实验研究. 计算机学报, 21(增刊): 86-91, 1998.8.
贺思敏, 张钹. 用吴方法求解可满足性问题I——算法变换. 计算机学报, 21(增刊): 79-85, 1998.8.
贺思敏, 卢旭光, 张钹. 局部搜索多初始点选择的划分策略的性能分析. 计算机学报, 21(增刊): 73-78, 1998.8.
名人名言
Elegant: simple but surprisingly effective.
— Cited by Dijkstra from Oxford Dictionary
The main motivation of a scientist is systematization.
— S. Chandrasekhar, Truth and Beauty
The real driving force for the scientist is wonderment about the complexity of the world we live in, and the hope that it can be described simply enough for us to understand, and elegantly enough to admire and enjoy.
— C.A.R Hoare, Unification —Unifying Theories, the Challenge for Computing Science
我国的古代数学基本上遵循了一条从生产实践中提炼出数学问题,经过分析综合,形成概念与方法,并上升到理论阶段,精练成极少数一般性原理,进一步应用于多种多样的问题。从问题而不是从公理出发,以解决问题而不是以推理论证为主旨,这与西方之以欧几里德几何为代表的所谓演绎体系旨趣迥异,途径亦殊。
— 吴文俊
复兴中国数学!(Rejuvenate Chinese Mathematics!)
— 吴文俊(Wu Wen-Tsun)
非名人名言
振兴中国的算法学!(Promote Chinese Algorithmics!)
— 贺思敏(He Si-Min)
算法就是生产力! (Algorithm is Productivity!)
— 贺思敏(He Si-Min)